二叉搜索树 C语言实现
1、二叉搜索树基本概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是一棵具有如下特性的非空二叉树:
(1)若它的左子树非空,则左子树上所有结点的关键字均小于根结点的关键字;
(2)若它的右子树非空,则右子树上所有结点的关键字均大于(允许的话,也可大于等于)根结点的关键字;
(3)左右子树本身又各是一个二叉搜索树。
根据二叉搜索树的特点知:对二叉搜索树进行中序遍历得到的结点序列必然是一个有序序列。
2、二叉搜索树的操作
下面通过详细程序展示二叉搜索树的操作
#include#include #define QueueMaxSize 20 //定义队列数组长度#define StackMaxSize 10 //定义栈数组长度typedef int ElemType;struct BTreeNode{ ElemType data; struct BTreeNode* left; struct BTreeNode* right;};//1、查找等于给定值x的元素,成功返回该结点值域的地址,否则返回NULL//a、递归方式:(消耗大量时间和空间)ElemType* Find(struct BTreeNode* BST, ElemType x){ if (BST == NULL) return NULL; else { if (x == BST->data) //若结点值等于x则返回结点值域的地址 return &(BST->data); else if (x < BST->data) return Find(BST->left, x); //向左子树继续查找并直接返回 else return Find(BST->right, x);//向右子树继续查找并直接返回 }}//b、非递归方式ElemType* Find1(struct BTreeNode* BST, ElemType x){ while (BST != NULL) { if (x == BST->data) //若结点值等于x则返回结点值域的地址 return &(BST->data); else if (x < BST->data) BST = BST->left; else BST = BST->right; } return NULL;}//2、更新:与查找算法相同,只需在返回之前先将找到的值替换再返回就行了,在此省略。//3、向二叉搜索树中插入元素x//a、递归方式:void Insert(struct BTreeNode** BST, ElemType x){ if (*BST == NULL) //在为空指针的位置链接新结点 { struct BTreeNode* p = malloc(sizeof(struct BTreeNode)); p->data = x; p->left = p->right = NULL; *BST = p; } else if (x < (*BST)->data) //向左子树中完成插入运算 Insert(&((*BST)->left), x); else Insert(&((*BST)->right), x); //向右子树中完成插入运算}//b、非递归方式void Insert1(struct BTreeNode** BST, ElemType x){ struct BTreeNode* p; struct BTreeNode* t = *BST, *parent = NULL; while (t != NULL) //为插入新元素寻找插入位置 { parent = t; if (x < t->data) t = t->left; else t = t->right; }//循环之后parent存储的是待插入位置的双亲结点 p = malloc(sizeof(struct BTreeNode)); p->data = x; p->left = p->right = NULL; if (parent == NULL) //若树为空,作为根结点插入 *BST = p; else if (x < parent->data) //链接到左指针域 parent->left = p; else parent->right = p; //链接到右指针域}//4、删除//a:删除叶子结点,只要将其双亲结点链接到它的指针置空即可。//b:删除单支结点,只要将其后继指针链接到它所在的链接位置即可//c:删除双支结点,一般采用的方法是首先把它的中序前驱结点的值赋给该结点的值域,//然后再删除它的中序前驱结点,若它的中序前驱结点还是双支结点,继续对其做同样的操作,//若是叶子结点或单支结点则做对应的操作,若是根结点则结束。int Delete(struct BTreeNode** BST, ElemType x){ struct BTreeNode* temp; temp = *BST; if (*BST == NULL) return 0; if (x < (*BST)->data) //带删除元素小于树根结点值,继续在左子树中删除 return Delete(&((*BST)->left), x); if (x > (*BST)->data) //带删除元素大于树根结点值,继续在右子树中删除 return Delete(&((*BST)->right), x); if ((*BST)->left == NULL)//待删除元素等于树根结点值且左子树为空,将右子树作为整个树并返回1 { *BST = (*BST)->right; free(temp); return 1; } else if ((*BST)->right == NULL)//待删除元素等于树根结点值且右子树为空,将左子树作为整个树并返回1 { *BST = (*BST)->left; free(temp); return 1; } else//待删除元素等于树根结点值且左右子树均不为空时处理情况 { if ((*BST)->left->right == NULL)//中序前驱结点就是左孩子结点时,把左孩子结点赋值给树根结点 //然后从左子树中删除跟结点 { (*BST)->data = (*BST)->left->data; return Delete(&((*BST)->left), (*BST)->data); } else//查找出中序前驱结点,把该结点值赋给树根结点,然后从中序前驱结点为根结点的树上删除根结点 { struct BTreeNode *p1 = *BST, *p2 = p1->left; while (p2->right != NULL) { p1 = p2; p2 = p2->right; } (*BST)->data = p2->data; return Delete(&(p1->right), p2->data); } }}//5、创建二叉搜索树,根据二叉搜索树的插入算法可以很容易实现void CreateBSTree(struct BTreeNode** BST, ElemType a[], int n){ int i; *BST = NULL; for (i = 0; i < n; i++) Insert1(BST, a[i]);}//6、二叉搜索树中可以直接用到二叉树中部分的操作,这里可以用到二叉树的输出、中序遍历和清除函数//这里只在需要的地方将其元素类型换为int,函数名后加上_int后缀,用来区分//输出二叉树,可在前序遍历的基础上修改。采用广义表格式,元素类型为intvoid PrintBTree_int(struct BTreeNode* BT){ if (BT != NULL) { printf("%d", BT->data); //输出根结点的值 if (BT->left != NULL || BT->right != NULL) { printf("("); PrintBTree_int(BT->left); //输出左子树 if (BT->right != NULL) printf(","); PrintBTree_int(BT->right); //输出右子树 printf(")"); } }}void Inorder_int(struct BTreeNode* BT)//中序遍历,元素类型为int{ if (BT != NULL) { Inorder_int(BT->left); printf("%d,", BT->data); Inorder_int(BT->right); }}void ClearBTree(struct BTreeNode** BT)//清除二叉树,使之变为一棵空树{ if (*BT != NULL) { ClearBTree(&((*BT)->left));//删除左子树 ClearBTree(&((*BT)->right));//删除右子树 free(*BT); //释放根结点 *BT = NULL; //置根指针为空 }}//主函数void main()//其中用到二叉树操作的函数都基本没变,只是元素类型换为int{ int x, *px; ElemType a[10] = {30,50,20,40,25,70,54,23,80,92}; struct BTreeNode* bst = NULL; CreateBSTree(&bst, a, 10); //利用数组a建立一棵树根指针为bst的二叉搜索树 printf("建立的二叉搜索树的广义表形式为:/n"); PrintBTree_int(bst); printf("/n"); printf("中序遍历:/n"); Inorder_int(bst); printf("/n"); printf("输入待查找元素值:"); scanf(" %d", &x);//格式串中的空格可以跳过任何空白符 if (px = Find(bst, x)) printf("查找成功!得到的x为:%d/n", *px); else printf("查找失败!/n"); printf("输入待插入元素值:"); scanf(" %d", &x); Insert(&bst, x); printf("输入待插入元素值:"); scanf(" %d", &x); Insert(&bst, x); printf("输入待插入元素值:"); scanf(" %d", &x); Insert(&bst, x); printf("进行相应操作后的中序遍历为:/n"); Inorder_int(bst); printf("/n"); printf("输入待删除元素值:"); scanf(" %d", &x); if (Delete(&bst, x)) printf("1/n"); else printf("0/n"); printf("进行相应操作后的中序遍历为:/n"); Inorder_int(bst); printf("/n"); printf("操作后的二叉搜索树的广义表形式为:/n"); PrintBTree_int(bst); printf("/n"); ClearBTree(&bst);}
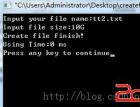
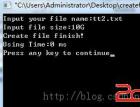
运行结果:

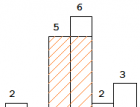
分析:此程序的初始二叉搜索树如下:

然后依次插入:35,45,41 三个元素,插入后的二叉搜索树如下:

最后删除元素为50的结点,删除结点后的二叉搜索树如下:

删除结点前的中序遍历为:20,23,25,30,35,40,41,45,50,54,70,80,92
删除过程:
需要删除的结点是:元素为50的结点,此结点为双支结点,我们知道其中序前驱结点(中序序列中处于它前面的一个结点)为45,所以将45替换到50的位置,
而45结点有一个左孩子,45结点为单支结点,则直接将其后续结点(此处为左孩子41)替换原45结点的位置。删除完成。
报名学习加微信/QQ 1602007,关注《东方联盟网》微信公众号
>更多相关文章
- 09-29如何通过wrap malloc定位C/C++程序的内存泄漏
- 02-25打车软件大战升级,补贴还能维持多久?
- 12-23BMP文件右旋90度[c语言]
- 12-23寻找直方图中面积最大的矩形(C语言版)
- 12-23[ndk,2]ndk开发案例和错误处理
- 12-23[ndk,1]ndk开发,C语言入门讲解
- 12-23C语言连续存储实现队列机制
- 12-23Objective-c 数据类型
首页推荐
佛山市东联科技有限公司一直秉承“一切以用户价值为依归
- 01-11全球最受赞誉公司揭晓:苹果连续九年第一
- 12-09罗伯特·莫里斯:让黑客真正变黑
- 12-09谁闯入了中国网络?揭秘美国绝密黑客小组TA
- 12-09警示:iOS6 惊现“闪退”BUG
- 03-29黑客组织攻击纽约大学官网,泄露 300万学生
- 03-29阿里妈妈广告自研AI模型LMA升级至万亿级参数
- 03-29筑牢食品安全防线 构建放心消费环境
- 03-29京东金融:数字人已累积服务超过500万用户
- 03-29京东外卖上线40天日订单破百万,入驻餐厅已
相关文章
24小时热门资讯
热门推荐
最新资讯
操作系统
黑客防御














 粤公网安备 44060402001498号
粤公网安备 44060402001498号