算法导论 之 平衡二叉树 - 删除[C语言]

一、前言概述

在之前的博文《算法导论 之 平衡二叉树 - 构造、插入、查询、销毁》和《算法导论 之 平衡二叉树 - 打印》中已经给出了构建、插入、查询、打印和销毁平衡二叉树的C语言实现过程，此篇中出现的相关结构体、宏、枚举、函数可以到以上两篇中查找。之所以现在才来写平衡二叉树的删除操作，主要是其过程相对比较复杂，且测试和实现过程中总是出现各种各样的问题，直到今天才彻底解决，平衡二叉树的处理终于可以告一段落。

二、处理思路

① 被删的节点是叶子节点

处理思路：将该节点直接从树中删除，并利用递归的特点和高度的变化，反向推算其父节点和祖先节点是否失衡。如果失衡，则判断是那种类型的失衡（LL、LR、RR、RL），再对失衡节点进行旋转处理，直到根节点或高度不再变化。

② 被删的节点只有左子树或只有右子树

处理思路：将左子树（右子树）替代原有节点的位置，并利用递归的特点和高度的变化，反向推算父节点和祖先节点是否失衡。如果失衡，则判断是那种类型的失衡（LL、LR、RR、RL），再对失衡节点进行旋转处理，直到根节点或高度不再发生变化。

③ 被删的节点既有左子树又有右子树

处理思路：找到被删节点的左子树的最右端的节点rnode，将rnode的值赋给node，再把rnode的左孩子替换rnode的位置，在把rnode释放掉，并利用递归特点，反向推断rnode的父节点和祖父节点是否失衡。如果失衡，则判断是哪种类型的失衡（LL、LR、RR、RL），再对失衡的节点进行旋转处理，直到根节点或高度不再发生变化。

三、代码实现

/****************************************************************************** **函数名称: avl_delete **功    能: 删除key值节点(对外接口) **输入参数:  **     tree: 平衡二叉树 **     key: 被删除的关键字 **输出参数: NONE **返    回: AVL_SUCCESS:成功 AVL_FAILED:失败 **实现描述:  **注意事项:  **作    者: # Qifeng.zou # 2013.12.19 # ******************************************************************************/int avl_delete(avl_tree_t *tree, int key){    bool lower = false; /* 记录高度是否降低 */    if(NULL == tree->root)    {        return AVL_SUCCESS;    }    return avl_search_and_delete(tree, tree->root, key, &lower);}

/****************************************************************************** **函数名称: avl_search_and_delete **功    能: 搜索并删除指定的key值节点(内部接口) **输入参数:  **     tree: 平衡二叉树 **     node: 以node为根节点的子树 **     key: 被删除的关键字 **输出参数:  **     lower: 高度是否降低 **返    回: AVL_SUCCESS:成功 AVL_FAILED:失败 **实现描述:  **注意事项:  **作    者: # Qifeng.zou # 2013.12.19 # ******************************************************************************/int avl_search_and_delete(avl_tree_t *tree, avl_node_t *node, int key, bool *lower){    avl_node_t *parent = node->parent;    /* 1. 查找需要被删除的节点 */    if(key < node->key)         /* 左子树上查找 */    {        if(NULL == node->lchild)        {            return AVL_SUCCESS;        }                avl_search_and_delete(tree, node->lchild, key, lower);        if(true == *lower)        {            return avl_delete_left_balance(tree, node, lower);        }        return AVL_SUCCESS;    }    else if(key > node->key)    /* 右子树上查找 */    {        if(NULL == node->rchild)        {            return AVL_SUCCESS;        }                avl_search_and_delete(tree, node->rchild, key, lower);        if(true == *lower)        {            return avl_delete_right_balance(tree, node, lower);        }        return AVL_SUCCESS;    }    /* 2. 已找到将被删除的节点node */    /* 2.1 右子树为空, 只需接它的左子树(叶子节点也走这) */    if(NULL == node->rchild)    {        *lower = true;        avl_replace_child(tree, parent, node, node->lchild);        free(node), node = NULL;        return AVL_SUCCESS;    }    /* 2.2 左子树空, 只需接它的右子树 */    else if(NULL == node->lchild)    {        *lower = true;        avl_replace_child(tree, parent, node, node->rchild)        free(node), node=NULL;        return AVL_SUCCESS;    }    /* 2.3 左右子树均不为空: 查找左子树最右边的节点 替换被删的节点 */    avl_replace_and_delete(tree, node, node->lchild, lower);    if(true == *lower)    {        avl_print(tree);        return avl_delete_left_balance(tree, node, lower);    }    return AVL_SUCCESS;}

/****************************************************************************** **函数名称: avl_replace_and_delete **功    能: 找到替换节点, 并替换被删除的节点(内部接口) **输入参数:  **     tree: 平衡二叉树 **     dnode: 将被删除的节点 **     rnode: 此节点最右端的节点将会用来替换被删除的节点. **输出参数:  **     lower: 高度是否变化 **返    回: AVL_SUCCESS:成功 AVL_FAILED:失败 **实现描述:  **注意事项:  **     >> 在此其实并不会删除dnode, 而是将rnode的值给了dnode, 再删了rnode. **         因为在此使用的递归算法, 如果真把dnode给释放了，会造成压栈的信息出现错误! **作    者: # Qifeng.zou # 2013.12.19 # ******************************************************************************/int avl_replace_and_delete(avl_tree_t *tree, avl_node_t *dnode, avl_node_t *rnode, bool *lower){    avl_node_t *parent = NULL, *rparent = NULL;    if(NULL == rnode->rchild)    {        *lower = true;                parent = dnode->parent;        rparent = rnode->parent;        dnode->key = rnode->key;    /* 注: 将rnode的值给了dnode */        if(rnode == dnode->lchild)        {            avl_set_lchild(dnode, rnode->lchild);            /* rnode->parent == dnode节点可能失衡，此处理交给前栈的函数处理 */        }        else        {            avl_set_rchild(rparent, rnode->lchild);            /* rnode的父节点可能失衡，此处理交给前栈的函数处理 */        }        free(rnode), rnode=NULL;    /* 注意: 释放的不是dnode, 而是rnode */        return AVL_SUCCESS;    }    avl_replace_and_delete(tree, dnode, rnode->rchild, lower);    if(true == *lower)    {        /* dnode的父节点可能失衡，此处理交给前栈的函数处理            但dnode可能使用，因此必须在此自己处理 */        avl_delete_right_balance(tree, rnode, lower);    }    return AVL_SUCCESS;}

/****************************************************************************** **函数名称: avl_delete_left_balance **功    能: 节点node的左子树某节点被删除, 左高度降低后, 平衡化处理(内部接口) **输入参数:  **     tree: 平衡二叉树 **     node: 节点node的左子树的某个节点已被删除 **输出参数:  **     lower: 高度是否变化 **返    回: AVL_SUCCESS:成功 AVL_FAILED:失败 **实现描述:  **注意事项:  **作    者: # Qifeng.zou # 2013.12.19 # ******************************************************************************/int avl_delete_left_balance(avl_tree_t *tree, avl_node_t *node, bool *lower){    avl_node_t *rchild = NULL, *rlchild = NULL, *parent = node->parent;    switch(node->bf)    {        case LH:    /* 左高: 左子树高度减1 树变矮 */        {            node->bf = EH;            *lower = true;            break;        }        case EH:    /* 等高: 左子树高度减1 树高度不变 */        {            node->bf = RH;            *lower = false;            break;        }        case RH:    /* 右高: 左子树高度减1 树失去平衡 */        {            rchild = node->rchild;            switch(rchild->bf)            {                case EH:    /* RR型: 向左旋转 */                case RH:    /* RR型: 向左旋转 */                {                    if(EH == rchild->bf)                    {                        *lower = false;                        rchild->bf = LH;                        node->bf = RH;                    }                    else if(RH == rchild->bf)                    {                        *lower = true;                        rchild->bf = EH;                        node->bf = EH;                    }                    avl_set_rchild(node, rchild->lchild);                    avl_set_lchild(rchild, node);                    avl_replace_child(tree, parent, node, rchild);                    break;                }                case LH:    /* RL型: 先向右旋转 再向左旋转 */                {                    *lower = true;                    rlchild = rchild->lchild;                    switch(rlchild->bf)                    {                        case LH:                        {                            node->bf = EH;                            rchild->bf = RH;                            rlchild->bf = EH;                            break;                        }                        case EH:                        {                            node->bf = EH;                            rchild->bf = EH;                            rlchild->bf = EH;                            break;                        }                        case RH:                        {                            node->bf = LH;                            rchild->bf = EH;                            rlchild->bf = EH;                            break;                        }                    }                    avl_set_rchild(node, rlchild->lchild);                    avl_set_lchild(rchild, rlchild->rchild);                    avl_set_lchild(rlchild, node);                    avl_set_rchild(rlchild, rchild);                     avl_replace_child(tree, parent, node, rlchild);                    break;                }            }            break;        }    }    return AVL_SUCCESS;}

/****************************************************************************** **函数名称: avl_delete_right_balance **功    能: 节点node的右子树某节点被删除, 左高度降低后, 平衡化处理(内部接口) **输入参数:  **     tree: 平衡二叉树 **     node: 节点node的右子树的某个节点已被删除 **输出参数:  **     lower: 高度是否变化 **返    回: AVL_SUCCESS:成功 AVL_FAILED:失败 **实现描述:  **注意事项:  **作    者: # Qifeng.zou # 2013.12.19 # ******************************************************************************/int avl_delete_right_balance(avl_tree_t *tree, avl_node_t *node, bool *lower){    avl_node_t *lchild = NULL, *lrchild = NULL, *parent = node->parent;    switch(node->bf)    {        case LH:    /* 左高: 右子树高度减1 树失去平衡 */        {            lchild = node->lchild;            switch(lchild->bf)            {                case EH:    /* LL型: 向右旋转 */                case LH:    /* LL型: 向右旋转 */                {                    if(EH == lchild->bf)                    {                        *lower = false;                        lchild->bf = RH;                        node->bf = LH;                    }                    else                    {                        *lower = true;                        lchild->bf = EH;                        node->bf = EH;                    }                    avl_set_lchild(node, lchild->rchild);                    avl_set_rchild(lchild, node);                     avl_replace_child(tree, parent, node, lchild);                    break;                }                case RH:    /* LR型: 先向左旋转 再向右旋转 */                {                    *lower = true;                    lrchild = lchild->rchild;                    switch(lrchild->bf)                    {                        case LH:                        {                            node->bf = RH;                            lchild->bf = EH;                            lrchild->bf = EH;                            break;                        }                        case EH:                        {                            node->bf = EH;                            lchild->bf = EH;                            lrchild->bf = EH;                            break;                        }                        case RH:                        {                            node->bf = EH;                            lchild->bf = LH;                            lrchild->bf = EH;                            break;                        }                    }                    avl_set_lchild(node, lrchild->rchild);                    avl_set_rchild(lchild, lrchild->lchild);                    avl_set_rchild(lrchild, node);                    avl_set_lchild(lrchild, lchild);                    avl_replace_child(tree, parent, node, lrchild);                    break;                }            }            break;        }        case EH:    /* 等高: 右子树高度减1 树高度不变 */        {            node->bf = LH;            *lower = false;            break;        }        case RH:    /* 右高: 右子树高度减1 树变矮 */        {            node->bf = EH;            *lower = true;            break;        }    }    return AVL_SUCCESS;}

/* # 检测节点的指针是否存在异常 # 很有效！ */void avl_assert(avl_node_t *node){    if((NULL == node)        || (NULL == node->parent))     {        return;    }    if((node->parent->lchild != node)        && (node->parent->rchild != node))     {        assert(0);    }    if((node->parent == node->lchild)        || (node->parent == node->rchild))    {        assert(0);    }}

四、处理结果

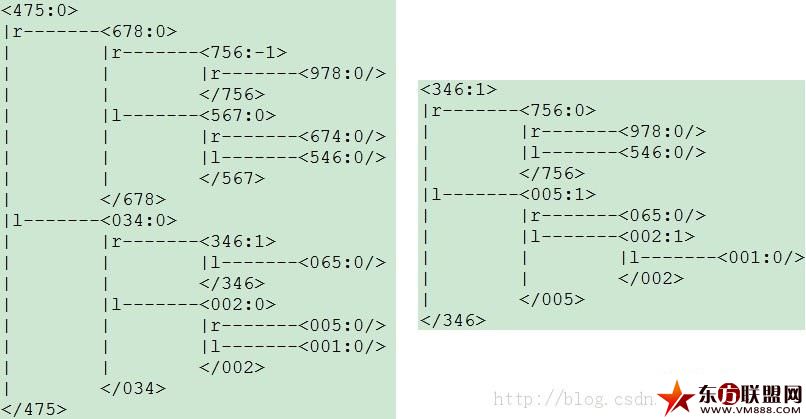
图1 测试结果

—— 邹祁峰

2013年12月20日 12时